HIGGS BOSON 2

Trần hồng Cơ .

Ngày 08 tháng 7 năm 2012 .

Dịch , tổng hợp biên soạn và tham khảo tài liệu từ các nguồn

1. Wikipedia .

2. The Encyclopedia of Science .

3. CERN .

4. ATLAS Experiments .

5. Compact Muon Solenoid CMS .

6. Scholarpedia .

Trong phần 1 chúng ta đã điểm sơ qua vài nét cơ bản về boson Higgs với các đề mục sau

1. HIGGS boson .

Vài nét sơ lược về boson Higgs .

2. Tính chất lý thuyết - Cơ chế Higgs .

Tóm tắt sự tương tác giữa các hạt được mô tả bởi mô hình tiêu chuẩn SM .

3. Cơ chế thay thế cho sự phá vỡ đối xứng điện yếu - Mô hình phi Higgs (Higgsless).

Đa sắc (Technicolor ) , Mô hình Higgsless nhiều chiều , Mô hình Abbott-Farhi, Lý thuyết top-quark ngưng tụ, Mô hình thắt .

4. Tìm kiếm thử nghiệm .

Phần tài liệu này là một sự kiện hiện tại. Thông tin có thể thay đổi nhanh chóng khi sự kiện tiến triển. (Tháng 7 năm 2012)

5. Mốc thời gian về bằng chứng thực nghiệm .

Tất cả các kết quả tham khảo với Standard Model Higgs boson, trừ khi có quy định khác.
-

Phần 2 sẽ chúng ta sẽ cùng đề cập đến cơ chế Higgs và cơ sở toán học của nó .

1. Cơ chế Englert-Brout-Higgs-Guralnik-Hagen-Kibble

Nguồn : http://www.scholarpedia.org/article/Higgs_boson#Eq-7

Bài viết này của giáo sư Thomas Kibble . Ông là một chuyên viên nghiên cứu cao cấp và giáo sư danh dự ngành Vật lý lý thuyết. Hướng nghiên cứu chính của ông là lý thuyết trường lượng tử và vũ trụ học, đặc biệt là những nghiên cứu về sự phá vỡ tính đối xứng và hình thành khuyết tật topo.
Ông là đồng chủ tịch của Quỹ khoa học Châu Âu Chương trình COSLAB ( Phòng thí nghiệm Vũ trụ học ) đến năm 2006 .

Nguồn : http://www3.imperial.ac.uk/people/t.kibble

Các cơ chế Englert-Brout Higgs-Guralnik-Hagen-Kibble cung cấp các phương tiện mà vec-tơ boson chuẩn ( gauge boson vector ) có thể đạt được khối lượng khác 0 trong quá trình phá vỡ đối xứng tự phát. Nó là một yếu tố quan trọng của lý thuyết điện yếu hình thành một phần Mô hình Chuẩn (SM) của vật lí hạt, và nhiều mô hình lý thuyết khác , chẳng hạn như lý thuyết trường thống nhất .

1.1 .Vai trò của cơ chế

Việc phát hiện ra cơ chế Englert-Brout Higgs-Guralnik-Hagen-Kibble loại bỏ một trở ngại lớn để xây dựng một lý thuyết thống nhất tương tác yếu và điện từ một cách hiệu quả . Vì những tương tác yếu là ngắn hạn và rất yếu ở năng lượng thấp, rõ ràng rằng nếu chúng đã được trung gian hóa bởi một vector trung gian boson W, thì nó phải có một khối lượng lớn - một vấn đề hiển nhiên , vì boson chuẩn được cho là có bản chất nó không có khối lượng, giống như photon. Một số cơ chế đã được yêu cầu để cung cấp khối lượng cho boson W, trong khi để lại những hạt photon không có khối lượng .
Ban đầu, cách gọi sự phá vỡ đối xứng tự phát đã được hiểu là để giới thiệu một vấn đề khác, đó là sự xuất hiện của các boson vô hướng Nambu-Goldstone không có khối lượng , dường như từ yêu cầu của định lý Goldstone (vì lý do sẽ được giải thích dưới đây). Tuy nhiên, hóa ra hai vấn đề này đều có một ý nghĩa là "hủy bỏ".
Cơ chế là một phiên bản tương đối một cách cơ bản , của một vật thể hoạt động trong một chất siêu dẫn. Nói ngắn gọn, thường được gọi là " cơ chế Higgs ", nhưng nói về thuật ngữ như vậy là không chính xác , bởi vì nó bỏ qua sự đóng góp của Englert & Brout (1964) được công bố ngay trước khi có những giả thiết về hạt Higgs (1964a, b), cũng như đã bỏ qua những đóng góp, độc lập của Guralnik, Hagen & Kibble (1964 ) và của những người trước đó, đặc biệt là Nambu (1960) và Anderson (1963).

1.2 Sự phá vỡ tính đối xứng tự phát .

Hình 1: hàm thế năng Sombrero với trạng thái không ổn định tại φ = 0 và cực tiểu xung quanh một vòng tròn.

Sự phá vỡ tính đối xứng tự phát xảy ra khi trạng thái cơ bản của một hệ thống không chia sẻ sự đối xứng đầy đủ dựa trên cơ sờ lý thuyết . Các ví dụ rõ ràng là của một sắt từ đẳng hướng, bao gồm một bảng các spin được gán vào các vị trí của lưới , và được mô tả bằng phiếm hàm Hamilton (1)

$H=-\frac{1}{2}\sum_{x,y}J_{x-y}S_{x}S_{y}$

Sx biểu thị spin ở vị trí lưới x . Cường độ của tương tác J chỉ phụ thuộc vào khoảng cách giữa các nút lưới x và y, và được giả định là giảm đi nhanh chóng khi khoảng cách này trở nên lớn. (Giả định này là quan trọng vì các lý do giải thích dưới đây.)
Mô hình này là bất biến theo một vòng quay đồng thời của tất cả các spin, và tương ứng với tổng số spin ký hiệu (2)

$S=\sum_{x}S_{x}$

Tổng số spin này được bảo toàn. Nhưng nếu J dương , thì rõ ràng trạng thái năng lượng thấp nhất là một trạng thái với tất cả các spin được sắp đặt cùng hướng (xem hình 2 (a)). Hướng trong đó các spin này chỉ ra là tùy ý. Như vậy có một trạng thái suy biến cơ bản. Việc thực hiện một vòng quay đồng thời của tất cả các spin sản sinh ra trạng thái cơ bản khác, với cùng mức năng lượng một cách chính xác (xem Hình 2 (b)).

Hình 2: (a) Một trạng thái cơ bản của sắt từ, với tất cả các spin được sắp đặt , (b) một trạng thái cơ bản khác, với tất cả các spin đều quay, (c) sự kích thích sóng -spin -năng -lượng -thấp .

Một hệ quả rất quan trọng về sự phá vỡ tính đối xứng tự phát của một tính đối xứng liên tục giống như trường hợp này , là có những kích thích có năng lượng tiến dần về 0 trong giới hạn bước sóng dài . Đây là những boson Goldstone hay Nambu-Goldstone boson. Ở trường hợp này đây cũng là các sóng spin, trong đó một vòng quay tuần hoàn phụ thuộc -không gian được áp dụng cho các spin (xem hình 2 (c)). Vì không tốn năng lượng để xoay tất cả các spin, từ (a) (b), nên cũng rất ít tốn năng lượng để làm cho sự thay đổi độ dài bước sóng tuần hoàn. Đây là nội dung của định lý Goldstone.

1.3 Mô hình Goldstone U(1) .

Lý thuyết trường tương đối đơn giản nhất ( theo Goldstone 1961) trình bày sự phá vỡ tính đối xứng tự phát như vậy là một trong những trường vô hướng phức φ với hàm mật độ Lagrange (3)

$L={\partial }_{\mu }\phi ^*{\partial }^{\mu}\phi-V(\phi)$

Trong đó (4)

$V(\phi)=m^2\phi^*\phi+\frac{1}{2}\lambda(\phi^*\phi)^2$

Dưới đây các đơn vị được chọn sao cho c = ℏ = 1, độ đo metric là (1, -1, -1, -1) và m và λ là khối lượng và hằng số bộ đôi tự tương tác của trường vô hướng. Mô hình này là bất biến dưới sự biến đổi toàn cục của các pha (5)

$\phi(x) \to \phi(x) e^{i\alpha }$

Tập hợp các biến đổi này xác định một nhóm đối xứng Abel U (1).
Vì vậy, khi m^2> 0, mô hình này chỉ là một trường vô hướng tự tương tác , có lượng tử là các hạt và phản hạt mang khối lượng m.Tuy nhiên mọi sự sẽ khác đi nếu m^2 <0 Khi đó , φ = 0 là giá trị của hàm thế V , đặc trưng cho một trạng thái cân bằng không ổn định với (6)

$V(\phi)=-\frac{1}{2}\lambda.v^2\phi^*\phi+\frac{1}{2}\lambda(\phi^*\phi)^2$

trong đó

$v^2=-\frac{2m^2}{\lambda}$

Điều này thường được gọi là hàm thế năng Sombrero (xem Hình 1 ) . Hàm này đạt cực tiểu trên đường tròn

$\left | \phi \right |^2=\frac{1}{2}v^2$

Vì vậy, trong trạng thái cơ bản, hoặc trạng thái chân không, người ta hy vọng giá trị của φ là 0 , với  độ lớn gần với    $v/\sqrt{2}$    , ngoại trừ các pha bất kỳ .
Sẽ có một họ suy biến trạng thái chân không đặt tên theo góc pha ký hiệu     $\left \ |0_{\alpha} \right \rangle$
Đối với sắt từ, tính đối xứng bị phá vỡ ngay cả trong thể tích hữu hạn. Đối với mô hình Goldstone, trạng thái có sự khác nhau đôi chút . Nếu hệ thống này đã bị giới hạn một thể tích hữu hạn, thì trạng thái chân không thực sự sẽ là một " sự chồng chất tuyến tính đối xứng của tất cả các trạng thái cân bằng ", trong đó giá trị kỳ vọng của φ vẫn sẽ triệt tiêu . Nhưng điều này không phải là trường hợp riêng cho một lý thuyết trường (về thể tích vô hạn).
Khi các trạng thái   $\left \ |0_{\alpha} \right \rangle$ là trực giao lẫn nhau thì tất cả các phần tử ma trận giữa những thể tích khác biệt sẽ gồm cả một số hữu hạn các trường triệt tiêu . Mỗi $\left \ |0_{\alpha} \right \rangle$ là trạng thái chân không của một không gian Hilbert riêng biệt được xây dựng bằng cách áp dụng các toán tử trường lên nó . (Lưu ý rằng các đại diện của mối quan hệ giao hoán hình nón này trên không gian Hilbert là không tương đương với biểu diễn không gian Fock - trái ngược với tình hình trong cơ học lượng tử thông thường nơi mà tất cả các biểu diễn tối giản của mối quan hệ giao hoán Heisenberg là tương đương Unitar )

Boson Nambu-Goldstone xuất hiện ở đây. Chúng ta có thể thấy điều này bằng cách chọn một điểm cực tiểu cụ thể, khi φ là thực và dương , và mở rộng về điểm đó (xem hình 3), xác định các trường dịch chuyển thực φ1, 2 bằng hàm (7) $\phi=\frac{1}{\sqrt2}(v+\varphi_1+i.\varphi_2)$

Hình 3: Định nghĩa của các trường dịch chuyển, biểu diễn cho sự biến đổ về trạng thái cân bằng ổn định (dấu chấm đỏ, bên phải), thay vì những điểm không ổn định (dấu chấm màu xanh lá cây, tâm đường tròn).

Hàm mật độ Lagrange tìm được có dạng (8) $L=\frac{1}{2}[({\partial }_\mu\varphi_1)^2+({\partial }_\mu\varphi_2)^2]-V$
Với hàm thế năng Sombrero (9)V=−18λv4+12λv2φ21+12λvφ1(φ21+φ22)+18λ(φ21+φ22)2.V=−18λv4+12λv2φ21+12λvφ1(φ21+φ22)+18λ(φ21+φ22)2.

$V(\phi)=-\frac{1}{8}\lambda.v^4+\frac{1}{2}\lambda.v^2.\varphi_1^2+\frac{1}{2}\lambda.v.\varphi_1(\varphi_1^2+\varphi_2^2)+\frac{1}{8}\lambda(\varphi_1^2+\varphi_2^2)^2$

Thành phần đầu tiên ở đây là chỉ đơn thuần là một hằng số không quan trọng. Bằng cách xây dựng như vậy , sẽ không có thành phần  tuyến tính, và, quan trọng, cũng không có thành phần chứa   $\varphi_2^2$
Bây giờ sự lượng tử hóa hình nón có thể tiến hành như bình thường theo các trường thành phần   φ1 , 2.
Mô hình này mô tả hai loại hạt , φ1 lượng tử khối lượng λ √ v  và  lượng tử φ2 không có khối lượng , với các bộ bậc 3 (cubic)  và bậc 4 (quartic) . Lượng tử φ2, tương ứng với những thay đổi không gian của góc pha, là boson Nambu-Goldstone.
Sự hiện diện của chúng được yêu cầu bởi định lý Goldstone trong bất kỳ lý thuyết về hiệp biến  Lorentz  hiển nào , trong đó một đối xứng liên tục bị phá vỡ tự phát . (Định lý này cũng đúng cho lý thuyết phi-tương đối cung cấp thêm một giả định được thỏa mãn , Điều này sẽ được thảo luận thêm dưới đây.)

1.4   Sự phá vỡ tự phát của đối xứng chuẩn cục bộ .

Đối xứng toàn cục  (5) có thể được thúc đẩy để một đối xứng địa phương được cung cấp một trường chuẩn tương ứng được giới thiệu đến , có thể nói rằng với một thế năng Aμ .
Phiếm hàm Lagrange  bây giờ có dạng (10)     $L=D_\mu\phi^*.D^\mu\phi-\frac{1}{4}F_\mu_\nu.F^\mu^\nu-V(\phi)$

trong đó đạo hàm hiệp biến và trường chuẩn được cho bởi $D_\mu\phi={\partial }_\mu\phi+ieA_\mu\phi$

và   $F_\mu_\nu={\partial }_\mu A^\nu-{\partial }_\nu A^\mu$

Phiếm hàm Lagrange này là bất biến
với biến đổi chuẩn cục bộ (11)    $\phi(x) \to \phi(x) e^{i\alpha(x)}$     và    $A_\mu(x) \to A_\mu(x)-\frac{1}{e}{\partial }_\mu\alpha(x)$

Đây là trường hợp đơn giản của các  lý thuyết chuẩn , với một nhóm chuẩn  Abel U (1).
Vì vậy, khi m^2> 0, đây  là hệ điện động lực vô hướng bình thường . Nó mô tả một hạt tích điện có khối lượng m, và phản hạt của nó, tương tác với các photon không có khối lượng. Nhưng điều gì sẽ xảy ra nếu m^2 là một lần nữa là số âm , có thể nói   $m^2=-\frac{1}{2}\lambda v^2<0$   sẽ giống như trước đây?
Ở đây cũng vậy, ta có thể thay thế (7), và thấy rằng V có dạng (9). Tuy nhiên, bây giờ có những thành phần bổ sung bậc hai phát sinh từ thành phần động học đầu tiên (10). Phiếm hàm Lagrange lúc này có dạng (12)
$L=\frac{1}{2}({\partial }_\mu\varphi_1 )^2+\frac{1}{2}({\partial }_\mu\varphi_2+evA_\mu )^2-\frac{1}{4}F_\mu_\nu F^\mu^\nu-\frac{1}{2}\lambda v^2\varphi_1^2+...$

các dấu chấm biểu thị điều kiện tương tác bậc 3 và 4 (và thành phần hằng). Bây giờ  rõ ràng rằng thành phần thứ hai cho trường chuẩn một khối lượng. Thật vậy, chúng ta có thể giới thiệu một trường mới   $B_\mu=A_\mu+\frac{1}{ev}{\partial }_\mu \varphi_2$

để các thành phần thứ hai trở thành một thành phần khối lượng cho Bμ, với khối lượng ev, và thành phần không có động lực cho trường φ2 còn lại.
Một cách khá gọn để mô tả tình huống là cần lưu ý rằng người ta có thể chọn một chuẩn để như vậy φ2 = 0, Aμ và Bμ trùng nhau (mặc dù điều cẩn thận là rất cần thiết với các điểm    $\phi=0$    ;  những điều này có liên quan với các khuyết tật topo).
Đây là một mô hình mô tả các trường khối lượng lớn, một trường vector Bμ với khối lượng ev, tương tác với  trường vô hướng φ1 , một lần nữa có khối lượng  là   λ √ v.
Trường chuẩn không khối lượng biểu kiến Aμ và trường vô hướng không khối lượng biểu kiến φ2 đã kết hợp với nhau để cho ra trường vector khối lượng Bμ .
Lưu ý rằng số lượng các trạng thái helicity là không thay đổi: hai trạng thái phân cực của Aμ và duy nhất một của φ2 kết hợp nhau để cung cấp cho ba trạng thái của Bμ. Đây là bản chất của cơ chế Englert-Brout Higgs-Guralnik-Hagen-Kibble .

1.5 Việc tránh khỏi định lý Goldstone .
-

Làm thế nào có thể đi đến lý thuyết các hạt không khối lượng, bất chấp định lý Goldstone là điều mà có vẻ như được yêu cầu phài có sự hiện diện của chúng ?
Chứng minh định lý

Để trả lời câu hỏi này, thật hữu ích để bắt đầu bằng cách kiểm tra một trong các chứng minh của định lý của Goldstone. Nó được dựa trên ba giả thuyết.
*Thứ nhất, lý thuyết phải có tính đối xứng liên tục, và một cách tương ứng dòng Noether   $j_\mu(x)$ được bảo tòan, đáp ứng   ${\partial }_\mu j^\mu =0$ .   Trong trường hợp của một trường vô hướng với đối xứng U(1) , dòng này là (13)
$j_\mu=-i\phi^*D_\mu\phi+i\phi D_\mu \phi^*$

*Thứ hai, đối xứng này bị phá vỡ tự phát , không có trạng thái  chân không bất biến , nhưng là một họ suy biến của các trạng thái chân không không- bất- biến . Cụ thể, đối với bất kỳ trạng thái chân không |0>, có tồn tại một trường $\phi$   (có thể tổng hợp) có  giá trị  kỳ vọng  chân không $\left \langle 0|\phi|0 \right \rangle$   là không bất biến. Lúc này tác tử Q của phép biến đổi là tích phân không gian của    $j^0$      (14)
$Q(t)=\int d^3 \textbf{x} j^0(t,\textbf{x})$
vì vậy điều có nghĩa là (15)       $-i\int d^3 \textbf{x}\left \langle 0|[j^0(0,x),\phi(0)]|0 \right \rangle\neq 0$
* Thứ ba , lý thuyết là hiệp biến Lorentz hiển ( manifestly Lorentz covariant ) .

Cách đơn giản nhất để chứng minh định lý là xét các biến đổi Fourier (16)
$f_\mu(k)=-i\int d^4 {x} e^{ikx}\left \langle 0|[j^\mu(x),\phi(0)]|0 \right \rangle\neq 0$
Điều kiện đối xứng bị phá vỡ (15) sau đó trở thành (17)
    $\int_{-\infty }^{\infty }dk^0 f^0(k^0,0)\neq 0$
Mặt khác, vì dòng được bảo toàn, chúng ta có (18)       $k_\mu f^\mu(k)=0$

Điều này cũng được yêu cầu trong trường hợp đặc biệt là (19)      $k^0 f^0(k^0,0)=0$
Từ phương trình (17) và (19) ta suy ra rằng    $f^0(k^0,0)$    chứa một tích khác 0 các biến phân    $\delta (k^0)$
Nếu chúng ta lồng thêm một tập đầy đủ các trạng thái trung gian vào  (16), sẽ thấy rằng điều này dẫn đến phải có những trạng thái liên kết chân không thông qua   $\phi$   mà $k^0 \to \0$ khi   k → 0, tức là, có các trạng thái hạt không có khối lượng.

1.6 Trường hợp đối xứng chuẩn .

Như vậy, làm thế nào để lập luận này không xảy ra trong trường hợp của một đối xứng chuẩn cục bộ ?
Điều quan trọng nằm trong giả thuyết thứ ba về hiệp phương sai hiển . Để lượng tử hóa một trường chuẩn , chúng ta phải chọn một chuẩn đánh giá , và áp đặt một điều kiện đo điều chỉnh cho một số trưởng hợp . Đối với lý thuyết chuẩn U (1), nếu muốn xây dựng trong một không gian Hilbert chỉ chứa trạng thái vật lý, điều này không thể được thực hiện theo cách hiệp biến hiển .
Lựa chọn đơn giản nhất là độ đo Coulomb, hoặc chuẩn bức xạ, được xác định bởi các điều kiện   ${\partial }_k A^k=0$ , đây là trường không-hiệp biến ( non-convariant ) vì nó phụ thuộc vào sự lựa chọn của trục thời gian.
Trong trường hợp này , sự chuyển mạch không bị yêu cầu phải triệt tiêu bên ngoài nón ánh sáng, và trong thực tế chỉ ra sự suy giảm giống như một dạng năng suất ngược. Do đó, phương trình liên tục    ${\partial }_\mu j^\mu=0$    không còn yêu cầu các toán tử (14) phải độc lập thời gian , bởi vì khi chúng ta tích phân từng phần thì sự đóng góp từ các thành phần bề mặt ở vô cực không cần phải triệt tiêu .
(Trong thực tế, tác tử Q không phải là thực sự được xác định rõ ràng, ngoại trừ bên trong các sự chuyển mạch.) Vì vậy, không còn suy ra được   $k_\mu f^\mu(k)=0$    . (Trong trường hợp phi- tương đối, giả thuyết thứ ba của định lý Goldstone là không có bao gồm lực tương tác xa , bởi vì điều đó đảm bảo rằng sự chuyển mạch suy giảm đủ nhanh ở vô cực mà tích phân bề mặt có thể bị giảm đi .)
Tất nhiên, có một sự thay thế cho cách hiệp biến hiển về sự lượng tử hóa trường điện từ, cụ thể là sử dụng chuẩn Lorentz, được xác định bởi     ${\partial }_\mu A^\mu=0$ .
Tuy nhiên trong trường hợp đó , không gian Hilbert nhất thiết phải chứa các trạng thái vô hướng phi- vật lý và photon theo chiều dọc . Ở đây định lý Goldstone chắc chắn sẽ được áp dụng, và tồn tại các boson không có khối lượng Nambu-Goldstone. Tuy nhiên, điều này quay lại vấn đề rằng chúng là những modes chuẩn hoàn toàn , không liên kết với các hạt vật lý theo  lý thuyết
Cơ chế này thường được nói đến như một sự trình bày  " tính đối xứng chuẩn bị phá vỡ tự phát ". Đó là một cách mô tả vắn tắt khá thuận tiện, nhưng thuật ngữ này có khả năng phần nào gây hiểu lầm. Quá trình lượng tử hóa đòi hỏi một sự lựa chọn một chuẩn , tức là, một sự phá vỡ đối xứng chuẩn rõ ràng . Tuy nhiên, kết quả lý thuyết không giữ lại một đối xứng pha toàn cục là cái bị phá vỡ tự phát bằng sự lựa chọn  pha $\left \langle \phi \right \rangle$ .
-
Tuy nhiên , điều rất quan trọng là các mô hình có nguồn gốc từ mô hình bất biến chuẩn đầy đủ ban đầu . Nói chung, các mô hình liên quan đến các trường vector khối lượng là không- tái chỉnh hóa được ( non- renormalizable ) . Nhưng lý thuyết trường chuẩn này là tái chỉnh hóa được, như đã được chứng tỏ bởi   't Hooft (1971) (xem lý thuyết gauge), chủ yếu bởi vì nó vẫn giữ được các đồng nhất thức Ward là cái đóng vai trò rất quan trọng trong khả năng tái chỉnh hóa trong điện động lực học lượng tử.

1.7 Sự phá vỡ đối xứng phi -Abel .

Về cơ bản các cơ chế tương tự có thể áp dụng trong trường hợp của một lý thuyết chuẩn phi- Abel.

Ví dụ đơn giản nhất là của một bộ ba của trường vô hướng, 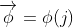$\overrightarrow{\phi}=\phi(j)$ , biến đổi theo biểu diễn liên hợp ba chiều của nhóm SO (3). Phiếm hàm Lagrange ở đây có dạng (20) $L=\frac{1}{2}\overrightarrow{D_\mu\phi}.\overrightarrow{D^\mu\phi}-\frac{1}{4}\overrightarrow{F_\mu_\nu}.\overrightarrow{F^\mu^\nu}-V(|\overrightarrow{\phi}|),$

Trong đó $\overrightarrow{D_\mu\phi}={\partial }_\mu\overrightarrow{\phi}+g\overrightarrow{A_\mu}\times \overrightarrow{\phi},$

và $\overrightarrow{F_\mu_\nu}={\partial }_\mu \overrightarrow{A}_\nu-{\partial }_\nu \overrightarrow{A}_\mu+g\overrightarrow{A}_\mu\times \overrightarrow{A}_\nu$

với g là hằng số liên kết chuẩn .

Phiếm hàm Lagrange này là bất biến theo biến đổi chuẩn SO (3), viết dưới dạng vi phân , $\delta \overrightarrow{\phi }=\overrightarrow{\delta w}\times \overrightarrow{\phi}$

và $\delta \overrightarrow{A}_\mu=\overrightarrow{\delta w}\times \overrightarrow{A}-\frac{1}{g}{\partial }_\mu\overrightarrow{\delta w}$ trong đó $\overrightarrow{\delta w}=(\delta w_j)$ là 3 tham số vi phân ( infinitesimal ) .

Bây giờ giả sử rằng V một lần nữa được chọn sao cho cực tiểu của nó không phải là φ điểm đối xứng 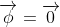$\overrightarrow{\phi}=\overrightarrow{0}$ nhưng trên một hình cầu bán kính khác 0 ,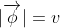 $|\overrightarrow{\phi}|=v$

Sau đó, như trước đây sẽ có là một họ suy biến các trạng thái chân không, đặc trưng bởi giá trị kỳ vọng chân không nằm trên mặt cầu. Ví dụ, một trong những trạng thái chân không như vậy sẽ có 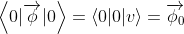$\left \langle 0|\overrightarrow{\phi}|0 \right \rangle=\left \langle 0|0|v \right \rangle=\overrightarrow{\phi_0}$ , có thể nói như vậy . Các điểm khác trên hình cầu sẽ tương ứng với những trạng thái chân không khác.

Trong trường hợp này, nhóm đối xứng SO (3) không bị phá vỡ hoàn toàn. Có một nhóm con không gián đoạn SO (2), bao gồm các phép quay trong mặt phẳng xy, với 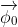$\overrightarrow{\phi_0}$ không thay đổi.

Trong trường hợp này, một trong ba boson chuẩn , thành phần $A_3 _ \mu$ tương ứng với đối xứng không gián đoạn này, vẫn không có khối lượng . Hai boson $A_1 _ \mu$ và $A_2 _ \mu$ có được khối lượng , bằng gv .

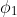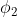Như trước kia các thành phần theo chiều dọc của các boson chuẩn khối lượng đến từ các Nambu-Goldstone boson $\phi_1$ và $\phi_2$ . Dao động trong hướng xuyên tâm ( hướng bán kính ) , được mô tả bởi 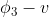$\phi_3-v$ , chính là các boson Higgs mang khối lượng .

1.8 Trường hợp của một nhóm đối xứng tổng quát .

Trong trường hợp tổng quát, giả sử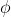 $\phi$ là bộ tích các trường thực 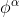$\phi^\alpha$ thuộc về một biểu diễn của nhóm đối xứng G với tác tử Hermit Ta (trong thực tế, là ảo và phản xứng) và tính đối xứng bị phá vỡ một cách tự phát giảm xuống nhóm con H khi ϕ đạt được giá trị kỳ vọng khác không ϕ0 . Sau đó, ta dễ dàng nhận thấy rằng ma trận khối lượng cho các trường vector là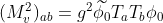 $(M_v^2)_a_b=g^2\widetilde{\phi_0}T_aT_b\phi_0$

trong đó dấu ~ là ký kiệu chuyển vị (transposition) . Những tác tử của H là tác tử của G thỏa mãn 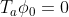$T_a\phi_0=0$ . Đối với chúng , các phần tử tương ứng của 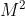$M^2$ triệt tiêu . Vì vậy , nếu G và H có số chiều là n và m , thì sẽ có m gauge boson ( boson chuẩn ) không có khối lượng và ( n - m ) boson có khối lượng .

Ví dụ, trong mô hình Weinberg-Salam, G=SU(2)×U(1) , H=U(1)

chúng ta có một boson chuẩn không khối lượng và ba boson chuẩn có khối lượng .

Một lần nữa, các thành phần theo chiều dọc của boson chuẩn có khối lượng đến từ những boson Nambu-Goldstone , trong khi các thành phần còn lại của ϕ (hay đúng hơn là của ϕ−ϕ0 ) sẽ đạt được khối lượng được cho bởi ma trận khối lượng vô hướng

$(M_s^2)_{\alpha\beta}=\left ( \frac{\partial^2 V}{\partial \phi^\alpha\partial \phi^\beta} \right )_{\phi=\phi_0}$

Đây chính là các Higgs bosons.

Mục đích chính của các cơ chế Englert-Brout Higgs-Guralnik-Hagen-Kibble là để cung cấp khối lượng cho các boson vector chuẩn . Tuy nhiên , một hiệu ứng phụ, là để cung cấp khối lượng các hạt cơ bản khác.

Bất kỳ fermion nào tương tác với trường vô hướng ϕ thông qua một thành phần tương tác có dạng 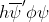$h\overline{\psi }'\phi\psi$ có thể có được một khối lượng, theo mức 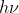$h\nu$ , bởi tác dụng của giá trị kỳ vọng khác 0 là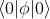 $\left \langle 0|\phi|0 \right \rangle$

Trong mô hình chuẩn, đây là cơ chế cung cấp khối lượng cho các lepton và các hạt quark. Yuy nhiên , đây vẫn là các thông số tùy ý , vì các khối lượng được xác định bởi các hằng số liên kết tùy ý h ; Ví dụ các hạt quark đứng đầu nặng bởi vì nó tương tác tương đối mạnh mẽ với trường Higgs.

Đôi khi có thể nói trường Higgs trao khối lượng cho tất cả các hạt khác, nhưng điều đó là không hoàn toàn chính xác. Điều quan trọng là cần lưu ý rằng hầu hết khối lượng của các nucleon đặc biệt không phát sinh theo cách này. Chỉ có khối lượng của các hạt quark là đến từ các cơ chế Englert-Brout Higgs-Guralnik-Hagen-Kibble . Phần lớn khối lượng nucleon đến từ một cơ chế dựa theo sự phác thảo trước đó của Nambu ( xem cơ chế Englert-Brout Higgs-Guralnik-Hagen-Kibble ( phần lịch sử) ).

2. Lý thuyết trường chuẩn - Gauge theories .

Nguồn : http://www.scholarpedia.org/article/Gauge_theories

Bài viết này của Viện sĩ Gerard 't Hooft .

Gerard 't Hooft sinh ngày 5 tháng 7 năm 1946 tại Den Helder, Hà Lan. Ông theo học chuyên ngành Vật lý và Toán học tại Đại học Utrecht, tốt nghiệp vào năm 1969. Ông nhận bằng Tiến sỹ năm 1972, với luận án của mình có tựa đề "Thủ tục tái chuẩn hóa cho các trường Yang-Mills". Ông nhanh chóng đạt được một học bổng hai năm tại CERN ở Geneva, và sau đó bổ nhiệm làm giáo sư tại Đại học Utrecht năm 1974, nơi ông đang cộng tác hiện nay.

Trong năm 1999, Tiến sĩ 't Hooft đã được trao giải Nobel Vật lý với đề tài "Để làm sáng tỏ cấu trúc lượng tử của tương tác điện yếu trong vật lý ", công trình này ông đã thực hiện cùng với M. Veltman , tiến sĩ khoa học hướng dẫn của ông . Tiến sĩ 't Hooft là Viện sĩ thông tấn nước ngoài của Viện Hàn lâm Khoa học Quốc gia Hoa Kỳ (1984) , thành viên danh dự nước ngoài của Viện Nghệ thuật và Khoa học (1986). Ông cũng là thành viên của Viện Hàn lâm Khoa học Hoàng gia Hà Lan (1982), nghiên cứu sinh của Viện Vật lý Anh (2000), Viện sĩ thông tấn nước ngoài Viện Hàn lâm Khoa học Quốc gia Pháp ( Académie des Sciences ) (1995). Tiến sĩ 't Hooft đã nhận được nhiều giải thưởng khác, bao gồm cả Wolf Prize năm 1982 và Huân chương 1986 Lorentz.

Cùng với Tiến sĩ Veltman, Tiến sĩ 't Hooft phát triển lý thuyết gauge. Điều này đã được chỉ ra rằng một số lý thuyết trường thành công là các lý thuyết gauge, bao gồm cả điện động lực học lượng tử và Mô hình Chuẩn. Ngoài ra, 't Hooft cũng quan tâm đến những gì có thể được suy ra về sự hấp dẫn lượng tử thông qua những nghiên cứu về các lỗ đen.

Nguồn : http://www.scholarpedia.org/article/User:Gerard_%E2%80%B2t_Hooft

Lý thuyết trường chuẩn có liên quan đến một lớp hoàn toàn tổng quát của các lý thuyết trường lượng tử được sử dụng để mô tả các hạt cơ bản và tương tác của chúng . Các lý thuyết được đặc trưng hóa bởi sự hiện diện của các trường vector, và như vậy là một sự tổng quát của lý thuyết cũ về Điện động lực học lượng tử (QED) được sử dụng để mô tả sự tương tác điện từ của các hạt cơ bản tích điện với spin 1/2. Bất biến chuẩn địa phương là một vấn đề rất trung tâm. Một tính năng quan trọng là những lý thuyết này thường là tái chỉnh hóa được khi được sử dụng trong không gian 3 chiều và 1 chiều thời gian .

2.1 Phương trình Maxwell và bất biến gauge ( bất biến chuẩn )

Ví dụ đơn giản nhất của một lý thuyết gauge là điện động lực, như đã được mô tả bởi các phương trình Maxwell. Cường độ điện trường 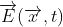$\overrightarrow{E}(\overrightarrow{x},t)$ và cường độ từ trường 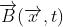$\overrightarrow{B}(\overrightarrow{x},t)$ tuân thủ các phương trình Maxwell thuần nhất (theo đơn vị SI) :

Theo bổ đề Poincaré, từ (2) kéo theo sự tồn tại một trường vector $\overrightarrow{A}(\overrightarrow{x},t)$ sao cho

Vì vậy (1) thành

chúng ta cũng có thể kết luận rằng có một trường thế $\overrightarrow{\Phi }(\overrightarrow{x},t)$ sao cho

trường Φ là trường điện thế ; trường vector $\overrightarrow{A}(\overrightarrow{x},t)$ được gọi là trường vector thế .

Cường độ của các trường thế này được xác định bởi các phương trình Maxwell không thuần nhất, là các phương trình có liên quan đến cường độ của các trường điện từ đến những điện tích và dòng điện tạo ra các trường này. Việc sử dụng các trường thế thường đơn giản hóa bài toán giải phương trình Maxwell.

Việc biến đổi lý thuyết này thành một lý thuyết gauge là một thực tế rằng các giá trị của các trường thế năng không hoàn toàn được xác định bởi các phương trình Maxwell .

Xét 1 cấu hình trường điện từ 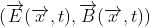$(\overrightarrow{E}(\overrightarrow{x},t),\overrightarrow{B}(\overrightarrow{x},t))$ , và Giả sử rằng nó được mô tả bởi các trường thế năng 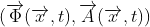$(\overrightarrow{\Phi}(\overrightarrow{x},t),\overrightarrow{A}(\overrightarrow{x},t))$ . Sau đó, sử dụng bất kỳ hàm vô hướng tùy ý 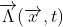$\overrightarrow{\Lambda }(\overrightarrow{x},t)$ , ta có thể tìm thấy một tập khác gồm các trường thế mô tả điện trường và từ trường, bằng cách viết

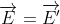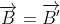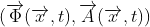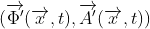Kiểm tra phương trình (3) và (5), một cách dễ dàng thấy $\overrightarrow{E}=\overrightarrow{E'}$ và $\overrightarrow{B}=\overrightarrow{B'}$ . Vì vậy, thiết lập $(\overrightarrow{\Phi}(\overrightarrow{x},t),\overrightarrow{A}(\overrightarrow{x},t))$ và $(\overrightarrow{\Phi'}(\overrightarrow{x},t),\overrightarrow{A'}(\overrightarrow{x},t))$ mô tả trạng thái vật lý tương đương . Bởi vì điều này, chúng ta gọi là phép biến đổi (6) là phép biến đổi gauge .

Vì 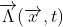$\overrightarrow{\Lambda }(\overrightarrow{x},t)$ có thể được lựa chọn là một hàm tùy ý các điểm 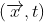$(\overrightarrow{x},t)$ trong không -thời gian, chúng ta có thể nói về một phép biến đổi gauge cục bộ . Thực tế là các trường điện là bất biến theo những phép biến đổi gauge địa phương nên lý thuyết của Maxwell được chuyển thành một lý thuyết gauge .

Trong lý thuyết trường lượng tử tương đối , trường 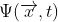$\Psi(\overrightarrow{x},t)$ của một hạt không tương tác và không spin (spinless) thường sẽ tuân theo phương trình

đơn vị được sử dụng như vận tốc của ánh sáng c = 1, và hằng số Planck ℏ = 1. Điều này cho phép các quan hệ phân tán giữa năng lượng và động lực quyết định bởi tính tương đối đặc biệt :

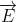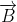Giả sử rằng các hạt trong câu hỏi mang một điện tích q. Làm thế nào để phương trình của nó sau đó bị ảnh hưởng bởi sự hiện diện của các trường điện từ? Nó chỉ ra rằng người ta không thể viết các phương trình chính xác bằng cách sử dụng các trường $\overrightarrow{E}$ và $\overrightarrow{B}$ trực tiếp. Thay vì vậy ở đây, người ta chỉ có thể chọn thêm các thành phần phụ thuộc vào các trường vector thế .

Có thể xác minh rằng phương trình này một cách chính xác đã sinh ra sóng bị chệch hướng bởi các lực điện từ theo cách mà ta mong đợi. Ví dụ, năng lượng E có thể dễ dàng nhìn thấy được tăng cường bằng một đại lượng $q\Phi(\overrightarrow{x},t)$ , là thế năng của một hạt tích điện trong một trường điện thế .

Tuy nhiên, những gì sẽ xảy ra đối với phương trình này khi thực hiện một phép biến đổi gauge ? Nó đã xuất hiện dường như là phương trình thay đổi để các lời giải cho trường ψ cũng thay đổi theo. Thật vậy, ψ thay đổi theo cách sau

Như vậy, trường ψ đã tạo ra một vòng quay (rotation) trong mặt phẳng phức . Điều này liên quan chặt chẽ đến một "thang biến đổi ", mà sẽ cho ra kết quả nếu ta để loại bỏ 'i' từ Eq. (10). Hermann Weyl, người đã lưu ý rằng phép biến đổi đối xứng này đơn giản là xác định lại thang của trường ψ , và giới thiệu từ 'đo' (hay chuẩn -gauge) để mô tả tính năng này.

Việc kết hợp sau đây

được gọi là đạo hàm hiệp biến, vì được lựa chọn theo cách như vậy để các đạo hàm của hàm 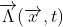$\overrightarrow{\Lambda }(\overrightarrow{x},t)$ bị loại ra trong phép biến đổi gauge :

Hình 1: Sơ đồ Feynman biểu diễn các electron phát ra một photon.

và điều này dễ dàng thấy rằng phương trình (10) mô tả cách ψ biến đổi theo một phép biến đổi gauge cục bộ , tuân theo cùng phương trình trường (9) cả trước và sau khi chuyển đổi (tất cả các thành phần trong phương trình được nhân cùng exp(- iqΛ) , để yếu tố đó là phi vật chất ).

Giá trị tuyệt đối, 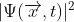$|\Psi(\overrightarrow{x},t)|^2$ không thay đổi dưới bất kỳ biến đổi gauge nào , và thực vậy , đây là các số lượng tương ứng với một điều gì đó có thể quan sát được một cách vật lý : các xác suất mà một hạt có thể được tìm thấy tại điểm 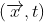$(\overrightarrow{x},t)$ . Một nguyên tắc chính là bất biến gauge địa phương yêu cầu tất cả các đạo hàm trong các phương trình của chúng ta để được thay thế bằng các đạo hàm hiệp biến .

2.2. Lý thuyết Yang-Mills .

Trong những năm 1950, ta biết rằng các phương trình trường proton, 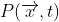$P(\overrightarrow{x},t)$ , và trường neutron, 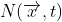$N(\overrightarrow{x},t)$ , là có thể quay các trường này trong một không gian phức hai chiều :

Hình 2: sơ đồ Feynman cho sự phát xạ của các photon Yang-Mills. Ảnh trên: electron chuyển thành en electron-neutrino, Ảnh dưới : neutron chuyển thành proton.

ma trận 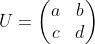$U=\begin{pmatrix} a & b\\ c & d \end{pmatrix}$ có thể chứa bốn số phức tùy ý, miễn là nó là ma trận Unitar 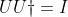$UU\dagger =I$ , và như thông thường, dịnh thức của U là 1.

Vì các phương trình này tương tự như phép quay có thể thực hiện trong không gian thường, để mô tả spin của một hạt, tính đối xứng trong vấn đề ở đây được gọi là đẳng spin ( isospin ) .

Vào năm 1954, C.N. Yang và RL Mills đã đưa ra một ý tưởng rất quan trọng. Ta có thể sửa đổi các phương trình theo cách mà các phép quay isospin này có thể được coi là phép quay gauge địa phương không ?

Điều này có nghĩa rằng, không giống như trường hợp đã được biết đến, ma trận U được phép phụ thuộc vào không - thời gian, giống như các tác tử gauge 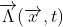$\overrightarrow{\Lambda }(\overrightarrow{x},t)$ trong cơ chế điện từ .

Yang và Mills cũng đã được lấy cảm hứng từ việc quan sát lý thuyết về trọng lực Einstein , Thuyết tương đối tổng quát , cũng cho phép những biến đổi tương tự như phép biến đổi gauge địa phương : sự thay thế hệ tọa độ khung bởi các hệ tọa độ khác một cách tùy ý, phụ thuộc vào không - thời gian.

Để viết các phương trình cho các proton và neutron, ta cần phải đạo hàm các trường này. Cách mà các đạo hàm này biến đổi theo một phép biến đổi gauge địa phương dẫn đến sẽ có các số hạng có chứa các gradients $\overrightarrow{\bigtriangledown }U$ ∇của ma trận U .

Để tạo ra các bất biến gauge- lý thuyết , các gradient phải được bỏ ra, và để làm điều đó, Yang và Mills thay thế các đạo hàm 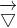$\overrightarrow{\bigtriangledown }$ bằng các đạo hàm hiệp biến

như đã được thực hiện trong cơ chế điện từ, xem phương trình (11).

Tuy nhiên ở đây các trường $\overrightarrow{A}(\overrightarrow{x},t)$ phải là có giá trị -ma trận , cũng giống như ma trận isospin U

Vì các ma trận U chứa bốn hệ số với một ràng buộc (định thức là 1), ta rút ra kết luận với một tập hợp của ba trường vector mới (có 3 vectơ thực độc lập trong ma trận (15)).Ở cái nhìn đầu tiên, chúng xuất hiện như là các trường của một hạt vector với isospin một . Trong thực hành , điều này sẽ tương ứng với các hạt với một đơn vị quay (tức là, hạt quay xung quanh trục của nó), và điện tích của nó có thể là trung tính hoặc +1 hoặc -1 . Do đó, lý thuyết Yang-Mills dự đoán và mô tả một loại hạt mới với spin một , truyền một lực không phải là không giống như lực điện từ.

Các trường tương đương với các trường điện và từ Maxwell đã thu được bằng cách xem xét hoán tử của hai đạo hàm hiệp biến :

trong đó các chỉ số μ, ν = 0,1,2,3, với 0 là đề cập đến thành phần thời gian.

Vì 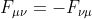$F_{\mu\nu}=-F_{\nu\mu}$ nên tensor này có 6 thành phần độc lập, 3 vector hình thành một điện trường và 3 vector hình thành một từ trường . Mỗi thành phần này cũng là một ma trận . Hoán tử [ Aμ, Aν ] là một thành phần phi tuyến mới làm cho các phương trình Yang-Mills phức tạp hơn rất nhiều so với các hệ thống Maxwell .

Ở khía cạnh khác, các hạt Yang-Mills, là lượng tử năng lượng của các trường Yang-Mills, tương tự như photon là lượng tử ánh sáng. Hạt Yang-Mills cũng không có khối lượng nội tại, và chuyển động với tốc độ ánh sáng. Thật vậy, các tính năng này cũng chính là lý do đầu tiên để bác bỏ lý thuyết này, bởi vì các hạt không có khối lượng thuộc loại này đã được phát hiện từ lâu, trong khi rõ ràng là chúng lại vắng mặt .

2.3 Cơ chế Brout Englert-Higgs .(BEH)

Lý thuyết này được hồi sinh khi nó được kết hợp với sự cố tự phát của đối xứng gauge địa phương, còn được gọi là cơ chế Brout Englert-Higgs. Xét một hạt vô hướng (spinless) được mô tả bởi một trường 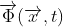$\overrightarrow{\Phi }(\overrightarrow{x},t)$ . Trường này được giả định là một trường vector, theo ý nghĩa mà nó trải qua một số phép quay khi một phép biến đổi gauge được thực hiện.

Trong thực tế, điều này có nghĩa là hạt mang một hoặc một số loại điện tích làm cho nó nhạy cảm với lực Yang-Mills, và thường có một số thành phần, có nghĩa là có nhiều loại khác nhau của lớp hạt này.

Những hạt như vậy phải tuân theo thống kê Bose-Einstein, là điều dẫn đến việc nó có thể trải qua sự ngưng tụ Bose-Einstein. Về trường ϕ , điều này có nghĩa như sau:

Trong chân không , trường ϕ có một giá trị không triệt tiêu F .

Hình 3: Sự phá vỡ tính đối xứng tự phát . Một vật cư trú trong một trường thế đối xứng quay tìm thấy một vị trí ổn định, không đối xứng. Trong trường hợp BEH , đó là trường Higgs, (ϕ1,ϕ2) tìm thấy một giá trị không đối xứng (F, 0) .

Sau một phép biến đổi gauge địa phương, điều này sẽ như sau

trong đó $U(\overrightarrow{x},t)$ là một trường ma trận đại diện cho phép biến đổi gauge địa phương.

, Do đó người ta thường nói rằng , chân không không phải là bất biến - gauge , nhưng điều này là không đúng. Trạng thái được mô tả bởi phương trình (18) là chân không giống như (17), nó chỉ được mô tả một cách khác nhau . Tuy nhiên, tính chất của chân không này có hệ quả quan trọng. Do thực tế rằng các trường quay mô tả trạng thái tương tự như giá trị trước đó, sẽ không có hạt vật lý nào khác liên quan đến trường quay.

Chỉ có chiều dài của vector ϕ là có ý nghĩa vật lý. Do đó, độ dài này là một bất biến gauge và chỉ có chiều dài của vector ϕ được liên quan đến một loại hạt cần phải trung hòa đối với các lực Yang-Mills. Hạt này được gọi là hạt Higgs.

Khi trường Higgs là một nguồn không đổi đối với cường độ trường Yang-Mills, thì phương trình Yang-Mills sẽ được sửa đổi bởi nó . Do trường Higgs, "photon" Yang-Mills ( được mô tả bởi trường Yang-Mills 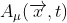$A_\mu(\overrightarrow{x},t)$ ) sẽ có được một khối lượng. Điều này cũng có thể được giải thích như sau. Photon không khối lượng chỉ có thể có hai trạng thái helicity , có nghĩa là, chúng chỉ có thể quay theo hai hướng . Điều này có liên quan đến thực tế vì ánh sáng có thể phân cực chính xác theo hai hướng. Những photon có khối lượng (các hạt không biến mất khối lượng và với một đơn vị spin ), luôn luôn có thể quay theo ba hướng . Chế độ quay thứ ba này được cung cấp bởi trường Higgs là cái mà bản thân nó mất đi một số của các thành phần vật lý . Tổng số của các thành phần trường vật lý vẫn như nhau trước và sau cơ chế Brout Englert-Higgs.

Một hệ quả nữa của hiệu ứng này về trường Yang-Mills là lực được truyền tải bởi các photon có khối lượng là một lực tầm ngắn (phạm vi của các lực tỉ lệ nghịch với khối lượng của các photon) . Các tương tác yếu có thể được mô tả thành công bởi lý thuyết Yang-Mills. Tập các phép biến đổi gauge địa phương hình thành các nhóm toán học SU(2)×U(1) . Nhóm này tạo ra 4 dòng của các photon (3 cho SU (2) và 1 cho U (1) ). Cơ chế Brout Englert-Higgs phá vỡ nhóm này theo cách mà một nhóm con của U(1) vẫn còn tồn tại . Đây là lý thuyết điện từ, chỉ với một photon. Ba photon khác trở thành có khối lượng , chúng có trách nhiệm đối với các tương tác yếu, mà trong thực tế để xuất hiện được yếu chỉ vì các lực này có một phạm vi rất ngắn . Với sự liên quan đến cơ chế điện từ , hai trong số các boson vector trung gian, W ±, có tích điện, và boson thứ ba , Z0, là trung hòa về điện . Khi sự tồn tại của trạng thái sau này được bắt nguồn từ các đối số lý thuyết nhóm , điều này đã dẫn đến dự đoán về một hình thức không được chú ý cho đến nay của tương tác yếu : đó là tương tác dòng trung hòa . Lý thuyết này, kết hợp cơ chế điện từ và lực yếu thành một, được gọi là lý thuyết điện-yếu ( electro-weak theory ), và đó là 1 lý thuyết đầy đủ có thể -tái chỉnh hóa đối với lực yếu (xem phần 5).

Hình 4: Sáu hương vị và màu sắc của các quark và phản hạt của chúng . Mũi tên cho thấy quá trình chuyển đổi yếu và mạnh

2.4 Sắc động lực lượng tử . ( Quantum Chromodynamics - QCD )

Khi đã được hiểu rằng các tương tác yếu, cùng với những tương tác điện từ, có thể được gán cho một lý thuyết gauge Yang-Mills, một câu hỏi được đặt ra là làm thế nào để giải quyết các lực mạnh , một lực rất mạnh với phạm vi hoạt động tương đối ngắn , là những yếu tố kiểm soát ứng xử của các hạt hadronic như các nucleon và các pions . Kể từ năm 1964 , người ta cũng hiểu rằng rằng những hạt này hành xử như là được xây dựng từ tiểu đơn vị , được gọi là quark. Ba loại quark được biết đến { up (u) , down (d) , và strange (s) } , và thêm ba quark sẽ được phát hiện sau này { charm (c) , top (t) và bottom (b) } .

Những hạt quark này có tính chất đặc biệt mà chúng vĩnh viễn dính lại với nhau , hoặc trong một bộ ba, hoặc một quark stick cùng với một hạt anti-quark. Tuy nhiên, khi chúng tiếp cận rất gần lẫn nhau , chúng lại bắt đầu ứng xử một cách tự do hơn là riêng rẽ .

Những tính năng này, chúng ta hiểu , một lần nữa , là do lý thuyết gauge Yang-Mills. Ở đây, chúng ta có nhóm toán học SU(3) là nhóm gauge địa phương, trong khi bây giờ tính đối xứng không còn bị ảnh hưởng bởi bất kỳ cơ chế Brout Englert-Higgs nào nữa . Do tính chất phi tuyến của trường Yang-Mills, nó tự tương tác, là cái đã làm cho các trường trong mô hình hoàn toàn khác với trường hợp điện từ : các đường xoáy ( vortex lines ) được hình thành, là cái tạo ra mối liên kết không thể phá vỡ giữa các quark . Ở khoảng cách gần, lực Yang-Mills trở nên yếu đi , và đây là một tính năng có thể được bắt nguồn một cách cơ bản từ việc sử dụng sự khuyếch nhiễu , nhưng nó là một tính chất của hệ thống lượng tử hóa Yang-Mills mà cho đến nay đã được cho là không thể dùng cho bất kỳ lý thuyết trường lượng tử nào , nó được gọi là sự tự do tiệm cận ( asymptotic freedom ). Việc phát hiện ra tính năng này có một lịch sử phức tạp.

Hình 5: Sơ đồ Feynman cho sự phát xạ của gluon QCD. Quark thay đổi màu sắc, nhưng hương vị của chúng vẫn như nhau: u vẫn là u và d vẫn là d.

Nhóm SU (3) dẫn đến rằng tất cả các loài của quark có ba loại, gọi là màu "đỏ", "xanh cây" hay "xanh dương". Do đó các trường của một quark là một vector 3 thành phần trong không gian nội tại 'màu sắc'. Phép biến đổi gauge Yang-Mills quay vector này trong không gian màu.

Các trường Yang-Mills tự hình thành ma trận 3x3 , với một ràng buộc ( vì định thức của ma trận xoay gauge Yang-Mills phải luôn bằng 1 ). Vì vậy, các trường Yang-Mills có 8 hạt giống như các photon mang màu sắc , gọi là các gluon. Những hạt Anti-quark sẽ mang màu sắc liên hợp ("màu lục lam", "màu đỏ tươi" hay "màu vàng"). Lý thuyết này được gọi là sắc động học lượng tử (QCD). Đây cũng là một lý thuyết tái chỉnh hóa được ( renormalizable ) .

Các gluon giữ các quark lại với nhau rất có hiệu quả theo một cách mà màu sắc của chúng có thể thêm lên đến tổng mới là màu trung hòa ("trắng" hoặc "màu xám"). Đây là lý do tại sao hoặc ba quark , hoặc một quark và một anti- quark ở gần nhau để tạo thành một hạt vật lý có thể quan sát được (hadron). Tính chất của lý thuyết này được gọi là tính giam giữ quark vĩnh viễn ( permanent quark confinement ) . Vì bản chất phi tuyến rất mạnh mẽ của các trường , nên sự giam giữ các hạt quark trong thực tế là khá khó khăn để chứng minh, trong khi tính chất tự do tiệm cận có thể được chứng minh một cách chính xác .

Thật vậy, một biểu diễn toán học đầy đủ về tính giam giữ quark , với các hiện tượng liên quan đến trạng thái khoảng trống khối lượng ( mass gap ) trong lý thuyết ( sự vắng mặt của các đối tượng hadronic hoàn toàn không khối lượng ) vẫn chưa được đưa ra, và đây là chủ đề chính để trao giải thưởng $ 1.000.000, - , do Viện Toán học Clay của Cambridge, Massachusetts đưa ra .

Hình 6: Các trường sắc động lượng tử ( quantum chromodynamical ) hình thành các xoáy giữ các hạt quark và antiquarks (bên trái) hoặc các hệ thống ba quark (bên phải) bị giam giữ vĩnh viễn .

2.5 Các phiếm hàm Lagrange ( Lagrangian ) .

Người ta không thể chọn tất cả phương trình trường theo ý thích. Các phương trình này phải tuân thủ các điều kiện như bảo toàn năng lượng. Điều này dẫn đến rằng có một nguyên lý hành xử ( action = reaction ), và nguyên lý này được thể hiện thuận tiện nhất là bằng các phiếm hàm Lagrange về lý thuyết.

Phiếm hàm Lagrange (chính xác hơn, hàm mật độ Lagrange ) 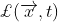$\pounds (\overrightarrow{x},t)$ là một biểu thức về các trường của hệ thống. Đối với một trường vô hướng Φ

và đối với trường Maxwell thì

trong đó tổng theo nghĩa tổng của các hiệp biến Lorentz qua các chỉ số Lorentz μ, ν .

Các phương trình trường tất cả có thể được trích xuất từ biểu thức này bởi yêu cầu tích hợp hoạt động

trong đó

là tổng các phiếm hàm Lagrange trong hệ thống , nó là tĩnh ( dừng ) với tất cả các biến phân ( infinitesimal variations ) của các trường này . Đây được gọi là nguyên lý Euler, Lagrange, và các phương trình là phương trình Euler-Lagrange . Đối với lý thuyết trường chuẩn ( gauge ) , điều này tổng quát hóa một cách trực tiếp , ta viết

sử dụng các biểu thức (16) cho các trường gauge Fμν, và cho tất cả các thành phần liên quan đến các trường khác được giới thiệu trước đó .Tất cả các tính đối xứng của lý thuyết này là các đối xứng của phiếm hàm Lagrange , và các chiều của tất cả các cường độ liên kết có thể dễ dàng được đọc tốt từ phiếm hàm Lagrange , đó cũng là điều quan trọng cho các thủ tục tái chuẩn hóa (xem phần kế tiếp).

2.6. Tái chuẩn hóa và Dị thường (Renormalization and Anomalies) .

Theo các định luật cơ học lượng tử, năng lượng trong trường chứa các gói năng lượng, và các gói năng lượng trong thực tế là các hạt quan liên quan đến trường này. Cơ học lượng tử đưa ra các quy định cực kỳ chính xác về cách mà những hạt tương tác , ngay sau khi các phương trình trường được biết đến và có thể được đưa ra trong các dạng của phiếm hàm Lagrange. Lý thuyết này sau đó được gọi lý thuyết trường lượng tử ( Quantum Field Theory -QFT), và nó giải thích không chỉ làm thế nào các lực được truyền qua việc trao đổi của các hạt, nhưng nó còn chỉ rõ rằng sự bội trao đổi ( multiple exchange ) có thể xảy ra .

Trong nhiều lý thuyết cũ, những bội trao đổi này đã dẫn đến những khó khăn: ảnh hưởng của chúng dường như không bị chặn, hoặc vô hạn . Tuy nhiên trong lý thuyết gauge , cấu trúc khoảng cách nhỏ được quy địnhrất chính xác theo của các yêu cầu của bất biến gauge . Trong lý thuyết như vậy người ta có thể kết hợp các hiệu ứng vô hạn của các bội trao đổi nhiều với việc tái định nghĩa khối lượng và điện tích của các hạt được bao gồm . Thủ tục này được gọi là sự tái chuẩn hóa.

Trong không - thời gian (3D+1T), hầu hết lý thuyết gauge đều tái chuẩn hóa được. Điều này cho phép chúng ta tính toán tác động của sự bội trao đổi các hạt với độ chính xác cao, như vậy nó cũng cho phép so sánh chi tiết với các dữ liệu thực nghiệm.

Hình 7: sơ đồ Feynman có chứa vòng lặp, do bội trao đổi hạt . Các vòng này thường tạo ra những biểu thức vô hạn.

Tái chuẩn hóa đòi hỏi khối và cường độ liên kết của hạt phải được xác định rất cẩn thận . Nếu tất cả các thông số liên kết của lý thuyết được đưa ra một chiều- khối lượng bằng 0 hoặc dương , thì số các biểu thức phân kỳ sẽ vẫn được kiểm soát . Thông thường , việc đòi hỏi lý thuyết còn lại bất biến gauge thông qua các thủ tục tái chuẩn hóa không để lại sự mơ hồ cho các định nghĩa. Tuy nhiên, thật là không rõ ràng khi các định nghĩa minh bạch về bất biến gauge tồn tại ở tất cả, vì bất biến gauge phải giữ lại cho tất cả các tương tác , trong khi chỉ có một vài biểu thức vô hạn là có thể được thay thế bởi những biểu thức hữu hạn .

Bằng chứng cho thấy cách thức và nguyên do các biểu thức tái chuẩn hóa rõ ràng có thể đạt được , một cách đẹp nhất có thể thu được , là việc xác nhận lý thuyết gauge có thể được hình thành trong bất kỳ số lượng các chiều kích không-thời gian nào .Thậm chí ta còn có thể xác định tất cả các sơ đồ Feynman rõ ràng cho các lý thuyết trong không gian nơi mà các chiều kích là 3−ϵ , trong đó ϵ là một đại lượng vô cùng bé .

Việc lấy giới hạn khi ε → 0 đòi hỏi sự trừ đi các cực có dạng Cn/ϵn từ các khối lượng "thô" ban đầu và thông số liên kết . Kết quả là một tập hợp các biểu thức bất biến gauge đơn nhất , hữu hạn. Trong thực tế, người ta thấy rằng thủ tục này, được gọi là sự qui chuẩn hóa chiều kích ( dimensional regularization ) và tái chuẩn hóa ( renormalization ) cũng thuận tiện để thực hiện các tính toán kỹ thuật phức tạp của sơ đồ vòng .

Tuy vậy , có một trường hợp đặc biệt, trong đó sự mở rộng những chiều kích khác từ một trường kinh điển là không thể . Điều này là khi các hạt fermion thể hiện tính đối xứng -Chiral ( Chiral symmetry ) . Tính đối xứng -Chiral là một sự đối xứng phân biệt các hạt quay trái và quay phải , và thực sự nó đóng một vai quan trọng trong Mô hình Chuẩn . Tính đối xứng -Chiral chỉ có thể có nếu không gian là 3 chiều, và do đó không cho phép sự tái chuẩn hóa chiều. Thật vậy , đối xứng -Chiral đôi khi không thể được bảo toàn khi tái chuẩn hóa lý thuyết.

Một dị thường xảy ra, được gọi là dị thường-Chiral . Lần đầu tiên hiện tượng này được phát hiện ra khi tính toán về biên độ phân rã π0 → γγ , đã có những câu trả lời không tuân theo theo mô hình đối xứng dự kiến .

Vì tính đối xứng gauge của Mô hình Chuẩn lại rất phân biệt những hạt quay trái và hạt quay phải (đặc biệt, chỉ những hạt neutrino quay trái là được tạo ra trong sự tương tác yếu), nên dị thường là một mối quan tâm lớn của các nhà vật lý .

Tuy nhiên cũng xảy ra như vậy , rằng các biên độ dị thường mà sẽ gây nguy hiểm cho bất biến gauge và vì thế , chạm đến tính tự nhất quán của các phương trình của chúng ta , tất cả đều được loại ra. Điều này có liên quan đến thực tế rằng một số phần mở rộng " tính thống nhất lớn" của Mô hình Chuẩn là được dựa trên những nhóm gauge tự do dị thường (xem phần 7).

Dị thường có một ý nghĩa vật lý trực tiếp. Một cấu hình trường topo xoắn được gọi là instanton (bởi vì nó biểu diễn cho một sự kiện tại thời điểm tức thời ), sẽ đại diện một cách chính xác cấu trúc trường gauge nơi đó dị thường là cực đại . Nó gây ra một sự vi phạm về việc bảo toàn một số những điện tích gauge . Khi có dị thường, thì ít nhất một trong những điện tích bao gồm không thể là một điện tích gauge , nhưng phải là một điện tích mà không có trường gauge nào được liên kết cả , giống như điện tich baryon .

Thật vậy , trong lý thuyết điện yếu, instantons kích hoạt sự vi phạm các định luật bảo toàn của baryon. Hiện nay người ta tin rằng điều này có thể giải thích sự mất cân bằng giữa vật chất và phản vật chất đã phát sinhtrong giai đoạn đầu của vũ trụ.

2.7 Mô hình chuẩn - Standard Model (SM ) .

Ngoài lực yếu, lực điện từ và lực mạnh, còn có lực hấp dẫn tác động lên các hạt cơ bản. Không có những lực cơ bản nào khác được biết. Ở cấp độ của các hạt đơn thuần , trọng lực là yếu nên nó có thể được bỏ qua trong nhiều trường hợp.

Giả sử bây giờ mà chúng ta lấy hệ thống Yang-Mills SU (2) x U (1) , cùng với trường Higgs, để mô tả lực điện từ và lực yếu, và bổ sung vào hệ này lý thuyết SU (3) Yang-Mills với lực mạnh , và chúng ta bao gồm tất cả các trường vật chất cơ bản được biết đến, là các hạt quark và lepton, với các quy tắc biến đổi phù hợp của chúng theo phép biến đổi gauge ; giả sử rằng chúng ta thêm vào điều này mọi cách có thể để các trường này có thể kết hợp, một tính năng quan sát thực nghiệm, có thể được xét như là một loại cơ bản của sự tự tương tác của các trường .

Khi đó, chúng ta sẽ thu được những gì được gọi là Mô hình Chuẩn . Nó là một trong những lý thuyết đo tuyệt vời mà theo nghĩa đen đại diện cho tất cả sự hiểu biết hiện tại của chúng ta về các hạt hạ nguyên tử và tương tác của chúng .

Mô hình Chuẩn công nhận cường độ của nó thực tế là nó có thể tái chuẩn hóa . Đó là chủ đề của rất nhiều thí nghiệm thực nghiệm và quan sát và đã trải qua tất cả những kiểm định khá tốt. Một sửa đổi quan trọng đã không thể tránh khỏi vào đầu những năm 1990: trong lĩnh vực lepton, các neutrino mang theo một lượng nhỏ khối lượng, và sự kết hợp của các trường .

Điều này không phải là hoàn toàn bất ngờ, nhưng những thí nghiệm neutrino rất thành công (đặc biệt là các thí nghiệm Kamiokande Nhật Bản) đã làm rõ ràng rằng những hiệu ứng này thực sự có thực. Chúng thực sự dẫn đến việc củng cố hơn nữa về Mô hình Chuẩn.

Một thành phần vẫn chưa được xác nhận : đó là các hạt Higgs. Quan sát về đối tượng này được dự kiến trong tương lai gần, đặc biệt là tại trung tâm Large Hadron Collider tại CERN, Geneva. Các phiên bản đơn giản nhất của Mô hình Chuẩn chỉ cần một điện hạt Higgs đơn nhất trung hòa điện , nhưng " các bộ phận Higgs " có thể là phức tạp hơn , vi dụ : hạt Higgs có thể nặng hơn nhiều so với dự kiến hiện nay , hoặc có thể tồn tại đa dạng, trong đó trường hợp các hạt vô hướng tích điện cũng sẽ được tìm thấy.

Mô hình Chuẩn không phải là hoàn hảo theo quan điểm toán học . Ở mức năng lượng rất cao (năng lượng cao hơn nhiều so với những gì có thể đạt được trong các máy gia tốc hạt ngày nay), lý thuyết trở nên trái tự nhiên . Trong thực tế, điều này có nghĩa là chúng ta không tin nữa rằng tất cả mọi thứ sẽ xảy ra chính xác theo quy định trong lý thuyết ; một hiện tượng mới lại sẽ được dự kiến . Các kịch bản phổ biến nhất là sự xuất hiện của một sự đối xứng mới gọi là siêu đối xứng ( supersymmetry ), tính đối xứng này liên quan giữa boson với fermion (các hạt như electron và hạt quark, những hạt yêu cầu phải áp dụng trường Dirac để mô tả chúng ).

2.8 Lý thuyết thống nhất lớn - Grand Unified .

Thật là tự nhiên khi nghi ngờ rằng lực điện yếu và lực mạnh cũng phải được kết nối bằng phép quay gauge . Điều này suy ra rằng tất cả các lực giữa các hạt hạ nguyên tử thực sự liên quan nhau bởi phép biến đổi gauge. Không có bằng chứng trực tiếp cho điều này, nhưng có một số trường hợp xuất hiện được chỉ ra theo hướng này. Trong phiên bản hiện tại của Mô hình Chuẩn, các trường SU (3) Yang-Mills, mô tả lực mạnh , thực sự cho thấy cường độ liên kết rất lớn, trong khi bộ phận U (1), mô tả phần điện (và một phần của các bộ phận yếu) , có cường độ liên kết nhỏ. Bây giờ chúng ta có thể sử dụng công cụ toán học về tái chuẩn hóa, đặc biệt cho cái gọi là nhóm tái chuẩn hóa , để tính toán cường độ hiệu quả của các lực này ở mức năng lượng cao hơn . Người ta tìm thấy là các lực SU (3) giảm cường độ , do tính tự do tiệm cận, nhưng cường độ liên kết U (1) lại gia tăng . Lực SU (2) thì thay đổi chậm hơn. Ở mức năng lượng cực cao, tương ứng với quy mô khoảng cách cực ngắn, khoảng 10^(-32) cm, ba cường độ liên kếtxuất hiện để tiếp cận một liên kết khác, như thể đó là nơi mà các lực hợp nhất lại .

Người ta tìm thấy là SU(2) × U(1) và SU (3) phù hợp khá độc đáo trong một nhóm được gọi là SU (5) . Chúng thực sự tạo thành một phân nhóm ( nhóm con ) của SU (5). Sau đó ta có thể giả định rằng một cơ chế Brout Englert-Higgs sẽ phá vỡ nhóm này thành nhóm con SU(2) × U(1) × SU (3) . Ta thu được cái gọi là lý thuyết trường thống nhất lớn ( Grand Unified Field theory ). Theo lý thuyết này, ta giả định ba thế hệ của các fermion, mỗi cái biến đổi trong cùng một cách dựa theo những phép biến đổi SU (5) . Tuy nhiên, lý thuyết SU (5) lại dự đoán rằng các proton có thể phân rã rất chậm, thành các lepton và pions. Sự phân rã này đã được tìm kiếm nhưng không thấy. Ngoài ra, trong mô hình này, cũng không phải là dễ dàng khi tính toán khối lượng neutrino và những phối hợp của nó. Một lý thuyết tốt hơn đã được tìm thấy , trong đó SU (5) được mở rộng thành SO (10) . Mô hình thống nhất lớn này đặt các neutrino ở cấp độ tương tự như các lepton điện tích. Thông thường, lý thuyết này được mở rộng đến một phiên bản siêu đối xứng.

2.9. Những lưu ý sau cùng .

Bất kỳ lý thuyết gauge nào cũng được xây dựng như sau. Trước tiên, chọn nhóm gauge. Điều này có thể là sản phẩm trực tiếp của bất kỳ số lượng các nhóm Lie bất khả quy, compact , hoặc là thuộc một trong chuỗi SU (N) , SO (N) hoặc Sp (2N) , hoặc các nhóm đặc biệt G2, F4, E6, E7, E8. Sau đó, chọn các trường fermionic (spin 1/2/) và trường vô hướng (spin 0) hình thành các đại diện của nhóm gauge địa phương này. Các thành phần Helicity bên trái và bên phải của các trường fermionic có thể là những đại diện khác nhau, miễn là các dị thường phải loại bỏ ra. Bên cạnh nhóm gauge địa phương, chúng ta có thể áp đặt chính xác và / hoặc gần đúng đối xứng toàn cục là tốt. Cuối cùng, chọn thành phần khối lượng và các điều kiện tương tác trong phiếm hàm Lagrange, được mô tả bởi các thông số liên kết điều chỉnh một cách tự do . Sẽ có chỉ có một số hữu hạn các thông số như vậy, với điều kiện là tất cả các tương tác được lựa chọn là thuộc các loại tái chuẩn hóa được , renormalizable (điều này có thể được đọc ra dễ dàng từ phiếm hàm Lagrange của lý thuyết ).

Có nhiều cách ( vô hạn )để xây dựng các lý thuyết gauge dọc theo những dòng này. Tuy nhiên, có vẻ như các mô hình hữu ích nhất để mô tả các hạt cơ bản quan sát, những mô hình tương đối đơn giản, dựa trên nhóm toán học cơ bản và các biểu diễn nhóm .Ta có thể tự hỏi tại sao Thiên nhiên dường như là đơn giản như vậy, và cho dù nó sẽ cứ như vậy khi các hạt mới và tương tác mới được phát hiện. Có thể hình dung, nhiều lý thuyết gauge phức tạp hơn sẽ được cần thiết để mô tả những tương tác ở mức năng lượng chưa đạt đến được trong các máy gia tốc hạt hiện nay. Các chủ đề có liên quan là lý thuyết Siêu đối xứng và lý thuyết siêu dây. Đây là những ý tưởng mới hơn về cấu trúc hạt và đối xứng hạt, nơi mà bất biến gauge cũng đóng một vai trò rất cơ bản.

References

Yang, C N and Mills, R L (1954). Conservation of Isotopic Spin and Isotopic Gauge Invariance. Physical Review 96: 191-195.
Higgs, P W (1964). Broken symmetries, massless particlees and gauge fields. Phys. Lett. 12: 132.
Higgs, P W (1964). Broken Symmetries and the Masses of Gauge Bosons. Phys. Rev. Lett. 13: 508.
Higgs, P W (1966). Spontaneous Symmetry Breakdown without Massless Bosons. Phys. Rev. 145: 1156.
Englert, F and Brout, R (1964). Broken Symmetry and the Mass of Gauge Vector Mesons. Phys. Rev. Lett. 13: 321.
Weinberg, S (1967). A Model of Leptons. Phys. Rev. Lett. 19: 1264.
Faddeev, L D and Popov, V N (1967). Feynman diagrams for the Yang-Mills field. Phys. Lett. 25B: 29.
't Hooft, G (1971). Renormalization of massless Yang-Mills fields. Nucl. Phys. B33: 173.
't Hooft, G (1971). Renormalizable Lagrangians for massive Yang-Mills fields. Nucl. Phys. B35: 167.
Taylor, J C (1971). Ward identities and charge renormalization of the Yang-Mills field. Nucl. Phys.B33: 436.
Slavnov, A (1972). Ward identities in gauge theories Theor. Math. Phys. 10: 153.
't Hooft, G and Veltman, M (1972). Regularization and renormalization of gauge fields. Nucl. Phys.B44: 189.
Adler, S L (1969). Axial-Vector Vertex in Spinor Electrodynamics Phys. Rev. 177: 2426.
Bell, J S and Jackiw, R (1969). A PCAC puzzle: π0→γγ in the σ-model Nuovo Cim. 60A: 47.
Adler, S L and Bardeen, W A (1969). Absence of Higher-Order Corrections in the Anomalous Axial-Vector Divergence Equation. Phys. Rev. 182: 1517.
Bardeen, W A (1969). Anomalous Ward Identities in Spinor Field Theories. Phys. Rev. 184: 1848.
Fritzsch, H; Gell-Mann , M and Leutwyler, H (1973). Advantages of the color octet gluon picture Phys. Lett. 47B: 365.
De Rujula, A; Georgi, H; Glashow, S L and Quinn, H (1974). Fact and fancy in neutrino physics. Rev. Mod. Phys. 46: 391.

TOÁN DỰ TRỮ

MỤC LỤC

Thứ Bảy, 10 tháng 1, 2015

HIGGS BOSON 2 .